Les mathématiques des carrés magiques

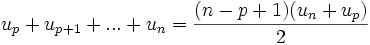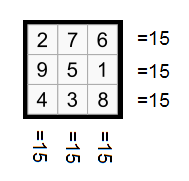
Simon de la LoubèrePierre de Fermat

Comment construire un carré magique?

Serge Frère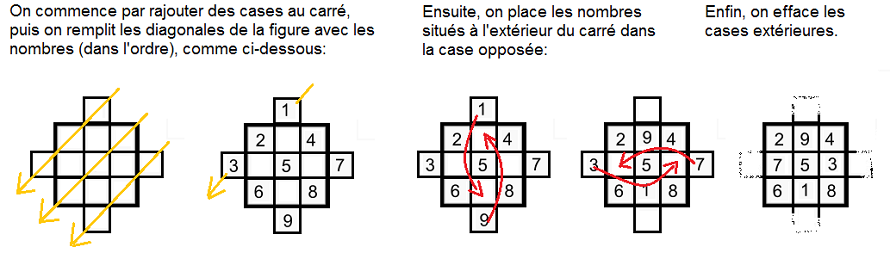
BABB'B"A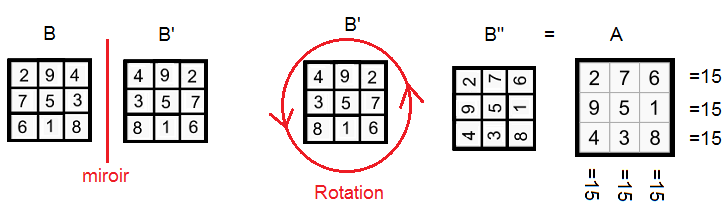

Les carrés magiques et les suites arithmétiques

Un carré magique arabe peint sur un bol chinois

A raison rrsuites arithmétiques
Il existe une infinité de suites arithmétiques, on peut par exemple considérer la suite suivante: 2   4   6   8   10   12  … Ici, chaque nombre se déduit du précédent en ajoutant « 2 ». On a donc r = 2.
On peut prendre n'importe quelles valeurs pour r et pour le point de départ de la suite, par exemple r = 103 et 8 comme point de départ. On a alors une suite arithmétique qui commence comme ça: 
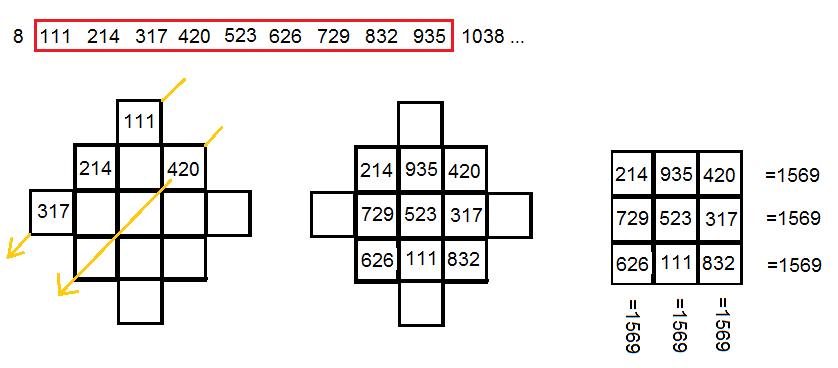
8, 111, 214, 317, 420, 523, 626, 729, 832, 935, 1038   ...
Pour construire un carré magique d'ordre 3, on peut utiliser n'importe quelle suite arithmétique, il suffit d'y choisir 9 nombres consécutifs. Voici un exemple construit avec la suite précédente:

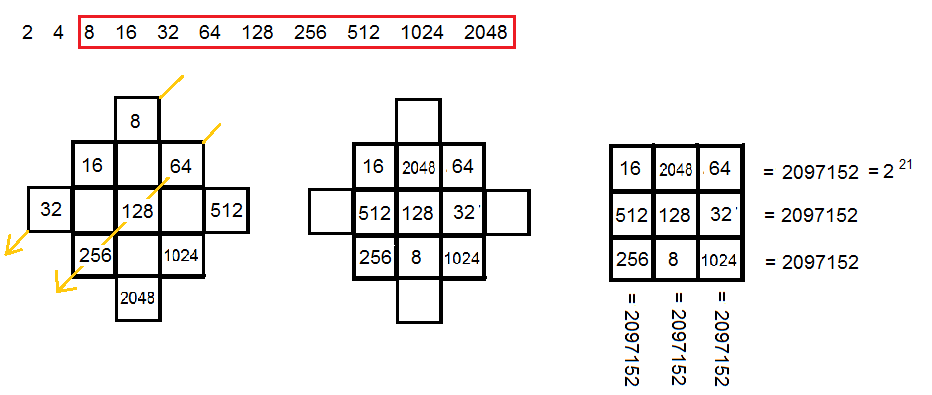
Les carrés magiques et les suites géométriques

géométriques
raisonqq




P=a³b³

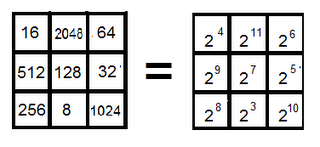
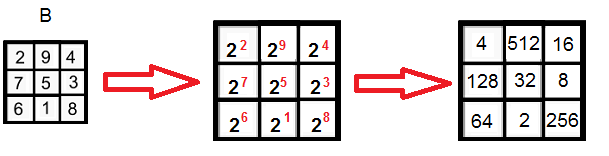
ab² 1 a²b

a² ab b²

b a²b² a

2 058 068 231 856 000 (Wikipédia

46 81 117 102 15 76 200 203

19 60 232 175 54 69 153 78

216 161 17 52 171 90 58 75

135 114 50 87 184 189 13 68

150 261 45 38 91 136 92 27

119 104 108 23 174 225 57 30

116 25 133 120 51 26 162 207

39 34 138 243 100 29 105 152

Des carrés magiques plus grands

Une plaque du 14 ème siècle gravée d'un carré magique d'ordre 6.

r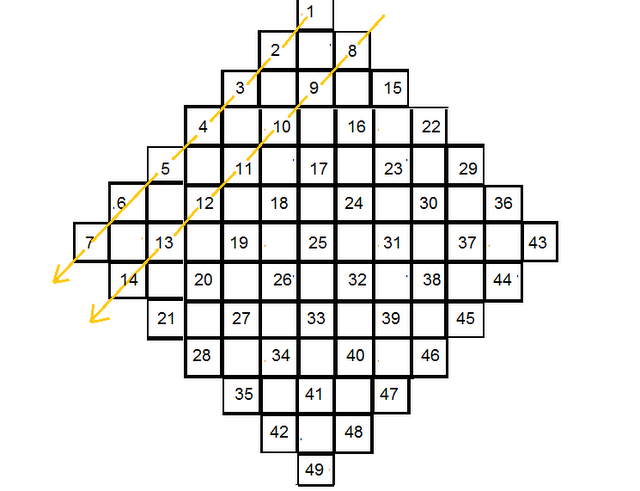

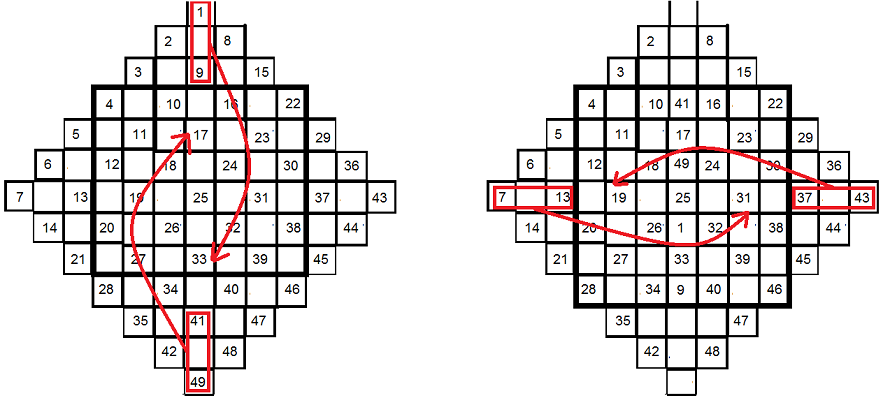
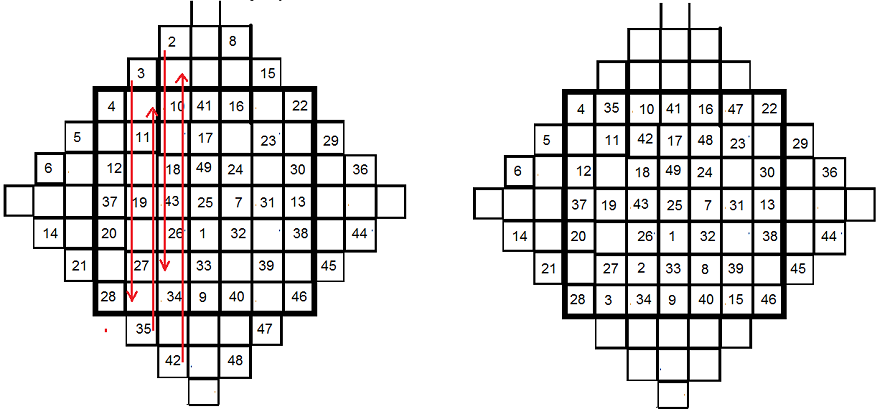
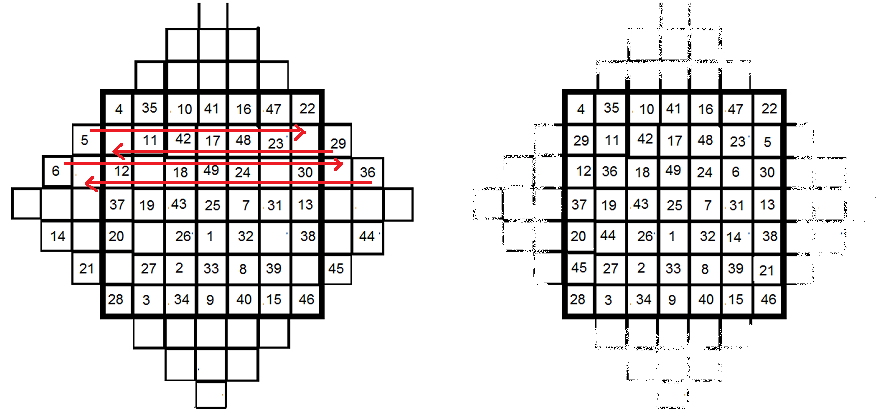
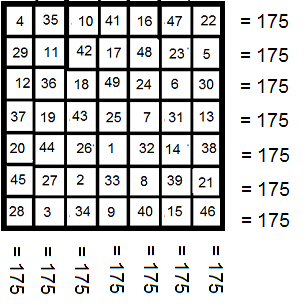
Les carrés d'ordre pair

Un carré magique d'ordre 4

cette page Parshvanath JainKhajuraho

7 12 1 14

2 13 8 11

16 3 10 5

9 6 15 4

Les cubes et les hypercubes magiques

. 

. nn n
Thérèse Eveilleau
cette page

Appendice: Calcul de la somme des termes d'une suite géométriques

Carl Friedrich Gauss Mozart
« Le jeune Gauss venait juste d'arriver dans cette classe quand Büttner donna en exercice la sommation d'une suite arithmétique. À peine avait-il donné l'énoncé que le jeune Gauss jeta son ardoise sur la table en disant « la voici ». Tandis que les autres élèves continuaient à compter, multiplier et ajouter, Büttner, avec une dignité affectée, allait et venait, jetant de temps en temps un regard ironique et plein de pitié vers le plus jeune de ses élèves. Le garçon restait sagement assis, son travail terminé, aussi pleinement conscient qu'il devait toujours l'être une fois une tâche accomplie, que le problème avait été correctement résolu et qu'il ne pouvait y avoir d'autre réponse.»

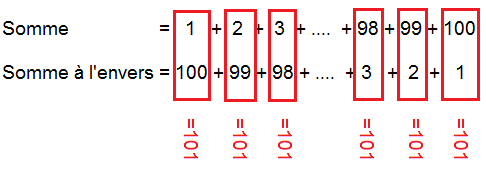
pnpnUnn^ème