Des mathématiques pour ''un enfant du siècle'' - 1

Charles-Louis de Chateauneuf hésitait entre les mathématiques, la religion et l'amour des femmes ...

Pourquoi – en 1833 - un jeune homme peut-il se passionner pour les mathématiques, alors qu'il est également attiré par l’irrationnel de la religion, et l'amour des femmes … ?

Charles-Louis est un enfant de ce siècle. Face à la mort demain, il y a la passion aujourd'hui. Si on exalte la sensibilité, l'imaginaire ; on reste dans un paysage réaliste : la nature, le corps, la beauté.

Victor Hugo en 1829

« le poète ne doit avoir qu'un seul modèle, la nature ; qu'un guide, la vérité » écrit Victor Hugo, en 1828, Préface de ''Odes et Ballades''.

« Il n’y a d’ailleurs aucune incompatibilité entre l’exact et le poétique. Le nombre est dans l’art comme dans la science. » V. Hugo

Le professeur de Charles-Louis, au collège royal de Limoges –-M. Gouré - l'avait initié au calcul différentiel ; en lui assurant que l'un de ses ''maîtres'' qu’était le professeur Augustin Cauchy (1789-1857), s'il était initié aux "Mathématiques transcendantes"...

Ce ''calcul différentiel '' - inventé par Newton et Leibnitz à la fin du XVII ème siècle - avait su fasciner l'imagination du jeune étudiant... Ce calcul correspondait alors à l’étude des dérivées, des tangentes aux courbes et des infiniment petits...

Son professeur avait excité sa curiosité avec des paradoxes comme ceux de Zénon:

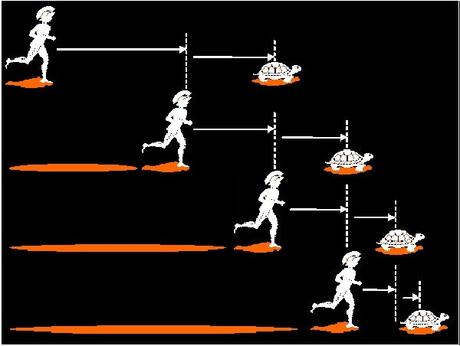
- le héros Achille qui logiquement ne peut dépasser à la course, la tortue: car il devra avant tout atteindre le point de départ de cette dernière.

Si l’espace est continu, on peut diviser chaque grandeur en deux, indéfiniment. Un point de vue atomiste considère que l'atome ( ou l'instant...) est indivisible... ces deux hypothèses restent paradoxales ...

L'erreur, ici est d'affirmer que la somme d’une infinité d’événements de plus en plus brefs tend vers l’infini, c’est-à-dire qu’Achille n’arrive jamais (temps infini) à rattraper la tortue.

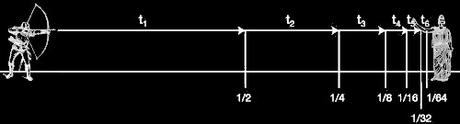
- la flèche: à chaque instant, la flèche se trouve à une position précise. Dans cet instant, la flèche n'a pas le temps de se déplacer elle reste immobile. Aux instants suivants, elle va rester immobile pour la même raison. Si le temps est une succession d'instants et que chaque instant est un moment où le temps est arrêté, le temps ne s'écoule donc pas. La flèche est donc toujours immobile à chaque instant et ne peut pas se déplacer. Considérant le temps comme une suite d'instants successifs, le mouvement est impossible.

Qu'est-ce donc que le temps? Si le temps est une suite d'instants successifs, le mouvement est impossible. S'il n’y a pas de temps entre deux instants consécutifs, alors la flèche devrait rester immobile ...!

A suivre ...